希拉德引擎 —— 由知识驱动的机器
‘Information is Physical’ – R. Landauer
「信息是物理存在的」—— 罗夫·兰道尔
The science of information was initially motivated not by interest in our physical universe, but rather by the blossoming field of computer science. It dealt with the manipulation of bits, 0’s and 1’s, and at outset, seemed to share little relation with the physical universe. Sure, most people believed that all information must be encoded in some physical medium (except perhaps the dualists who regarded the mind as separate from the brain), but it had little direct relevance to concepts such ass force, energy, or any of other myriad of observables that’s traditionally associated with the physical world.
所谓信息科学,一开始并不是由我们的物理世界启发的,而是蓬勃发展的计算机科学。它和「操作比特」打交道,比特, 也就是0和1。总体来看,它和物理世界似乎没什么关联。当然,大部分人相信所有的信息都必须由物理媒介所承载(也许除了那些二元论者,他们相信心灵和大脑彼此独立)。不过它也的确和那些物理概念没什么直接联系,比如力、能量,或者传统的物理世界里面其它不尽其数的可观测的东西。
Yet, remarkably, the mere knowledge, or possession of bits, can be directly related to such quantities. This relation is no better demonstrated than Szilard’s engine, whose fuel is only information… and nothing else.
然而,值得一提的是,所谓知识,或者「拥有比特」这件事本身,可以直接关联到这些物理量上。没什么比希拉德引擎更适合展示这种直接关联了,这引擎的燃料是纯粹的信息……再没别的了。
The mechanics of it is simple to describe. We consider a single gas molecule trapped in a chamber of volume \(V=LA\) where \(L\)is the length of the chamber, and \(A\)is its cross-sectional area. The chamber is in thermal equilibrium with the outside environment at some temperature \(T\). From statistical mechanics, we know that gas molecules obeys the Ideal Gas Law:
\(\displaystyle PV=kT\)
Where \(P\)is the pressure it exerts, and \(k\)is Boltzmann’s constant. Since all components are in thermal equilibrium, the second law of thermal dynamics seems to suggest that there exists no possible way to extract work from the system… however, what if we were capable of measuring the location of the gas particle inside at each point in time?
希拉德引擎的力学原理描述起来非常简单。想象一个单独的气体分子被放在一个容器里,容器的体积\(V=LA\)其中,\(L\)是容器的长度,\(A\)是容器的横截面面积。这个容器与外界达到了热力学平衡,它们的温度是\(T\)。由统计力学我们知道这个气体分子此时遵守理想气体状态方程:
\(\displaystyle PV=kT\)
其中\(P\)是压强,\(k\)是玻尔兹曼常数。由于系统中的每一个部分都处于热力学平衡状态,根据热力学第二定律,这个系统没有任何可能对外做功……但是,如果我们能够随时知道这个气体分子在容器里的位置呢?
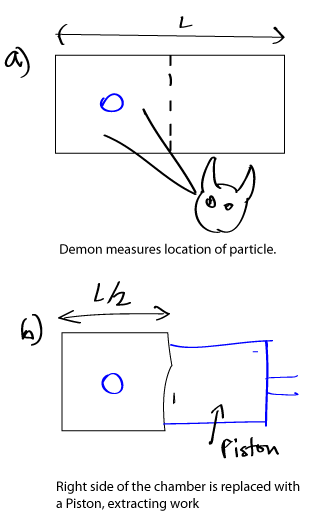
Consider Maxwell’s demonstration, who is capable of doing just that. When he sees that molecule on the left hand side of the chamber, he quickly drops down a shutter that separates the chamber into two separate compartments. The demon then inserts a piston into the right side chamber and releases the shutter. Since the pressure in the left chamber is now double the pressure outside, we would expect the gas molecule inside then slowly pushed the piston till its pressure once again equalizes that of the environment. Clearly, if the demon were to attach the piston to some machine, work can be extracted … In particular, we know that the work done \(W\), obeys \(W = \int F(x)dx\). Substituting the observation that \(F(x)=AP(x)\), and the ideal gas law, we have:
\(\displaystyle W = kT\int_{L/2}^L\frac{dx}{x}=kTln2\)
Thus, each cycle of this engine produces \(kTln2\) Jules of energy… from a system that is in thermal equilibrium.
是时候请出「麦克斯韦妖」了,它刚好可以做到这件事。当它看到气体分子在容器的左半边时,他就迅速地降下一个挡板把容器分成左右两个部分。这个怪物随后在容器的右半部分放进一个活塞,然后打开刚刚那个挡板。此时容器左边的压强是外界压强的两倍,我们可以想象到,气体分子会推动活塞,直到容器的压强再次和环境的压强相同。很显然,如果这妖怪把活塞和什么机器连接起来,这个系统就可以这么做功了……具体来说,我们知道所做的功\(W\) 可以这么计算: \(W = \int F(x)dx\). 根据我们的实际情况代入力的表达式 \(F(x)=AP(x)\), 然后代入理想气体状态方程, 我们就得到了:
\(\displaystyle W = kT\int_{L/2}^L\frac{dx}{x}=kTln2\)
也就是说,这台引擎的一次循环可以产生 \(kTln2\) 焦耳的能量…… 从一个处于热力学平衡的系统当中。
Wait, what did you say! Alarm bells should sound immediately. The initial and final state of the system appears exactly identical, and yet we have extracted energy from the system. Is this finally the perpetual motion machine that everyone is dreaming of?
等一下,你刚刚说了什么?!警报声应该立即响起。系统的初始和最终状态看起来完全一样,然而我们还是从这个系统中提取出了能量。难道这就是所有人都梦寐以求的永动机吗?
To solve this paradox, we must look closely at each of the individual operations. Somewhere within the sequence, energy must have been discretely injected into our engine … but where? The laws of physics for any closed system is reversible, and thus our approach is to identify whereabouts of the irreversible operation hides. The obvious candidates seem the measurement process, or perhaps the installation of the shutter or piston. Yet, while such actions are likely to be irreversible in practice, there’s no reason why they need to be in principle … elastic collisions can function as measurements, and everything else can be adiabatically. So at outset, it looks like the second law of thermodynamics has indeed been shattered!
为了解决这个悖论,我们必须仔细审视一下这里面的每一个操作步骤。在这一系列操作中,一定在哪一步有能量被偷偷注入到我们的引擎里了……但是,是在哪一步呢?在任何封闭系统里面,物理学定律都是可逆的,所以我们的任务就是找到那个不可逆的操作藏在哪里。最显然的怀疑对象是测量过程,也可能是挡板的引入或者活塞。不过,尽管这些操作在实际应用中很可能是不可逆的,原则上,它们并不必须如此……弹性碰撞可以用于测量,其它部分也可以找到类似的方法。所以最终来看,热力学第二定律确确实实被打破了!
There is however, one component of the system we’ve so far failed to address … the demon himself. Somewhere within the mind of this demon, he will need to store the knowledge of the result of his measurement – whether the gas molecule in question is in the left or right side of the chamber. Provided we regard this mind as being physical, it can be modeled by having to demonstrate store his knowledge of some physical system with two configurations – a single bit, with states 0 and 1. Each cycle of the Szilard requires the demon to assign a value to the one bit depending on the result of his measurement, and there fore erase whatever value was stored in the bit previously. This assignment process… mapping both 0 and 1 to a single value, is fundamentally irreversible.
然而系统中还有一个部分我们没有考虑到……那只妖怪。在它意识中的某处,它必然要储存它的测量结果——即那个气体分子到底在容器的左半边还是右半边。假设我们认为这个「意识」是物理的,那么我们可以建立这样的模型:这只妖怪要把它的知识存储在一个有两种配置的物理系统中——一个比特,状态要么是0要么是1。希拉德引擎的每一个循环,这只妖怪都要根据它的测量结果给这个比特赋予一个数值。也就是说,得擦除这个比特先前存储的数值。这个赋值的过程……把无论先前的0或是1修改成新的那个数值,从根本上来说,是不可逆的。
The Energy Cost of Deleting Information:
删除信息需要的能量代价
In 1961, Landauer’s published a remarkable argument that energy is indeed required to erase information. Take, for example, the single bit that the demon holds. A physical process that assigns a specific value to the bit must first erase the previous value from memory. Whatever physical process that enacts this erasure, it must work equally well regardless of whether the bit is in state 0 or state 1. The initial system exists in two possible configurations, and thus possesses an entropy of \(kln2\). After erasure, the system exists in a single state, and hence has entropy 0. This, the entropy of the system has decreased.
在1961年,兰道尔发表了他著名的论断:擦除信息实际上确实是需要能量的。让我们拿那个麦克斯韦妖的一个比特来举例。给那个比特赋予数值的物理过程首先必须从内存(妖怪的记忆)中擦除先前的数值。无论是什么样的物理过程,它在擦除时,无论这个比特处于状态1还是0,都一定工作得一样良好。系统初始时(测量之前)可能处于两种状态,因此系统的熵为\(kln2\)。擦除之后(测量之后),系统确定地存在于某种状态,熵变为了0。这样,系统的熵实际上减少了。
Landauer argued, on the basis of that entropy does not decrease, that this loss of entropy must correspond to a gain of at least \(kln2\) units of entropy elsewhere. Thus, the acting of erasing the information would incur \(kTln2\) Jules. Coincidentally, this is the exact amount of energy generated by the Szilard’s engine at each cycle.
兰道尔的论断中说,在熵不可能凭空减少的基础上,这个熵减一定在别的什么地方对应着至少 \(kln2\)个单位的熵增。也就是说,擦除信息,向系统中贡献了\(kln2\)焦耳。巧合的是,这恰恰是希拉德引擎在每个循环中能够产生的能量。
Information, theoriotically, it appears, has saved us from a rather embarrassing perpetual motion machine!
信息,理论上讲,看起来,成功地从那个令人尴尬的永动机手里拯救了我们!
Although Szilard’s engine does not allow us to generate energy out of nothing, it does provide that subtle link between energy and information. Mere knowledge of the state of a system gives us the capacity to extract power from it. The catch is that the mere storage of that knowledge requires power. There’s only a net gain if our hard drive lives in a colder environment than the engine, and thus a temperature gradient is still required for work.
尽管希拉德引擎并不能让我们凭空产生能量,它却实实在在地揭示了能量和信息之间的某种微妙联系。关于一个系统状态的纯粹的知识,给了我们从中汲取能量的能力。问题是储存这份知识需要能量。只有当我们的硬盘所处的环境比引擎温度更低时,才可能有能量的正收益。然而,这依然需要构造一个温度梯度。